Երկկենցաղները ցամաք դուրս եկած առաջին ողնաշարավոր օրգանիզմներ են: Այս դասին պատկանող բոլոր կենդանիները հասուն վիճակում շնչում են թոքերով, ունեն եռախորշ սիրտ և արյան շրջանառության երկու շրջան: Ողնաշարավորների ենթատիպում երկկենցաղները ամենասակավաթիվ օրգանիզմներն են, ունեն մոտ 4,5 հազար տեսակ:
Երկկենցաղները ձվադրում են ջրում: Այստեղ է անցնում նաև նրանց կյանքի թրթուրային շրջանը: Միայն կերպարանափոխվելուց և հասուն ձևի վերածվելուց հետո նրանք կարող են ապրել ցամաքում: Դրանով էլ պայմանավորված է դասի անվանումը:
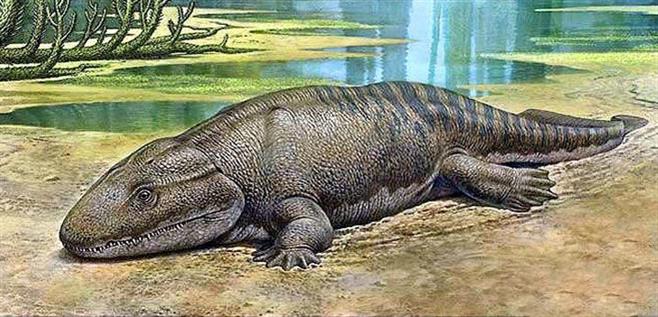
Մոտավորապես 300 մլն տարի առաջ երկրագնդի կլիման շոգ էր, հետևաբար ջրամբարները ցամաքում էին և աղքատանում թթվածնով: Այդ պայմաններում հնագույն վրձնալողակ ձկները, դուրս գալով ցամաք, հավանաբար սկիզբ տվեցին հնադարյան առաջին երկկենցաղներին՝ ստեգոցեֆալներին:
Երկկենցաղները տարածված են բոլոր աշխարհամասերում՝ բացի Անտարկտիդայից: Նրանք ապրում են լճերի, գետերի ափերին, ստվերոտ ու խոնավ անտառներում, ճահճոտ վայրերում: Երկկենցաղները ակտիվ են ջրում օրվա բոլոր ժամերին, ցամաքում օրվա մեծ մասն անցկացնում են արևի ուղղակի ճառագայթումից պատսպարվելով: Ցամաքում գիշերը երկկենցաղները դուրս են գալիս որսի:
Երկկենցաղները սառնարյուն կենդանի օրգանիզմներ են:
Այդ իսկ պատճառով նրանք ակտիվ են միայն տարվա տաք եղանակներին: Բազմացման շրջանում նրանք մոտենում են ջրամբարին: Այնուհետև ձմեռում են կա՛մ ջրամբարի հատակին, կա՛մ ցամաքի վրա՝ թաքստոցներում, քարերի տակ և այլն:
Երկկենցաղների մեջ տարբերում ենք.
անպոչ երկկենցաղներ՝ դոդոշներ, գորտեր, ծառագորտեր:
պոչավոր երկկենցաղներ՝ տրիտոններ, սալամանդրաներ:
անվերջույթ երկկենցաղներ՝ որդուկներ:
Ցամաքային կենսակերպով պայմանավորված երկկենցաղների համար հատուկ կարևորություն է ստացել մաշկը:
Երկկենցաղների մաշկը մերկ է, զուրկ է թեփուկներից: Սակայն դրա փոխարեն այն հարուստ է լորձ արտադրող գեղձերով: Որոշ երկկենցաղների լորձը խիստ թունավոր է, որի համար նրանք որս չեն դառնում այլ գիշատիչների համար: Հարավային Ամերիկայի փոքրիկ ծառագորտի մեկ առանձնյակի լորձը բավական է 1500 մարդ սպանելու համար:
Այն օգտագործում էին ացտեկներն ու մայաները՝ թունավոր նետեր պատրաստելու համար:
Լորձը պաշտպանում է մաշկը բակտերիաներից և փոշուց: Լորձի շնորհիվ երկկենցաղների մաշկի մակերեսին առաջանում է հեղուկ թաղանթ, որի մեջ լուծվում է մթնոլորտային թթվածինը:
Ուշադրություն
Մաշկի չորանալու դեպքում գորտը շնչահեղձ է լինում թթվածնի պակասից:
Բացի թթվածնի կլանումից՝ գորտը մաշկով արտաքին միջավայրից կլանում է ջուր, քանի որ գորտերը ջուր չեն խմում բերանով:
Երկկենցաղներին բնորոշ է հովանավորող և նախազգուշացնող գունավորումը:
Առաջինով նրանք ձուլվում են միջավայրին և դառնում աննկատ, իսկ երկրորդով զգուշացնում իրենց վտանգավոր լինելու մասին:
Երկկենցաղների մարմինը կազմված է միմյանց սահուն հաջորդող գլխից և մարմնից, որոշ երկկենցաղների մոտ մարմնի շարունակություն է հանդիսանում նաև պոչը:
1. Գլուխ. սահմանազատվում է իրանից թմբկաթաղանթներով՝ կրում է տեսողական և լսողական զգայարանները, բերանը, քթանցքները, որոնցում գտնվում են նաև հոտառական պարկերը, գանգատուփում գտնվում է գլխուղեղը:
2.Իրան. սահմանազատվում է պոչից հետանցքով՝ կրում է առջևի և հետին զույգ ցամաքային վերջույթների գոտիները, ներքին օրգանները: Իրանի վրա տարբերակում ենք մեջք և փորիկ:
3.Պոչ. բնորոշ է միայն սալամանդրաներին և տրիտոններին: Բոլոր երկկենցաղները տեղաշարժվում են վերջույթներով:
4. Վերջույթներ՝
առջևի վերջույթներ – հիմնականում ծառայում են ցամաքի վրա հենվելու համար:
ետին վերջույթներ – ծառայում են ցատկելու և ջրում լողալու համար: Պոչավոր երկկենցաղների մոտ դրանք ևս հենվելու և ցամաքում քայլքով տեղաշարժվելու համար են:
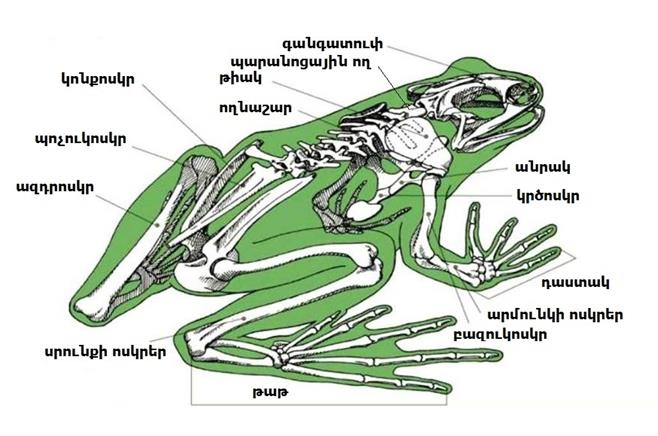
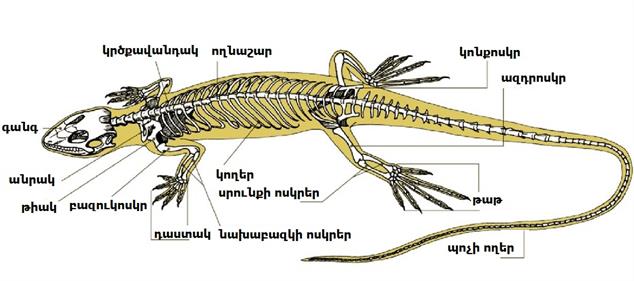
Ի տարբերություն ձկների՝ երկկենցաղները, պայմանավորված ցամաքային կենսակերպով, ունեն առավել զարգացած և մասնագիտացած կմախք:
Երկկենցաղների կմախքը ունի հետևյալ հիմնական բաժինները` 𝐼. գանգ, 𝐼𝐼. ողնաշար, 𝐼𝐼𝐼. գոտիներ, 𝐼𝑉. վերջույթներ:
𝐼.Գանգ. կազմված է գանգատուփից, որը պաշտպանում է գլխուղեղը ծնոտներից, և պարունակում է ավելի քիչ քանակով մանր ոսկրեր, քան ձկները:
𝐼𝐼.Ողնաշար. ունի 4բաժին՝ պարանոցային, իրանային, սրբանային, պոչային:
Պարանոցային և իրանային ողերը ունեն վերին աղեղներ, որոնք ձևավորում են ողնաշարային խողովակը, որտեղ տեղակայված է ողնուղեղը: Պարանոցային և սրբանային ողերից յուրաքանչյուրը կենտ ող է: Պարանոցային ողի միջոցով գլուխը շարժուն միացած է ողնաշարին: Սրբանային ողի միջոցով կոնքագոտին միանում է ողնաշարին, դրանով իսկ ամուր հենարան ստեղծելով ետևի վերջույթների համար: Պոչային ողերը պոչավոր երկկենցաղների մոտ լավ արտահայտված են և կազմում են ողնաշարի շարունակությունը, սակայն վերին աղեղներ չունեն: Անպոչ երկկենցաղների մոտ սերտաճել են՝ առաջացնելով պոչոսկր:
𝐼𝐼𝐼. Գոտիներ
Առջևի գոտի՝ ուսագոտի – կազմված է կենտ կրծոսկրից, զույգ անրակից, զույգ թիակից:
Հենարան է հանդիսանում առջևի վերջույթների համար:
Ետևի գոտի՝ կոնքագոտի – կազմված է միմյանց միացած երեք զույգ մասերից:
Հենարան է հանդիսանում հետևի վերջույթների համար:
𝐼𝑉. Վերջույթներ
Բոլոր ողնաշարավորների նման երկկենցաղներն ունեն զույգ վերջույթներ՝
Առջևի վերջույթներ – կենտ բազուկոսկր, զույգ նախաբազկի ոսկրեր, դաստակ, 4 ազատ մատներ:
Ետևի վերջույթներ – կենտ ազդոսկր, զույգ սրունքի ոսկրեր, թաթ, լողաթաղանթով միացած 5 մատներ:
Երկկենցաղների իրանի մկանների մի մասը պահպանել է հատվածավորությունը ձկների նման: Լավ զարգացած են անպոչ երկկենցաղների վերջույթների, իսկ պոչավորների՝ պոչի մկանները: Ձկների համեմատությամբ բարդացել են նաև երկկենցաղների բերանի և լեզվի մկանները: Այդ իսկ պատճառով մի շարք երկրներում, օրինակ՝ Ֆրանսիայում, գորտի տոտիկները համարվում են խորտիկ:
Սողունները ցամաքը գրաված առաջին ողնաշարավոր օրգանիզմներ են: Սողունները ցամաքային կենսապայմաններին լավագույնս հարմարվել են պատմական զարգացման ընթացքում: Ի տարբերություն երկկենցաղների՝ նրանք հիմնական կախում չունեն ջրից: Նրանք առաջացել են հնագույն երկկենցաղներից՝ ստեգոցեֆալներից: Մինչև 1 մ երկարություն ունեցող, ճահճային կենսակերպով բրածո կենդանի սեյմուրիան կարող է համարվել հնադարյան սողունների նախահայրը: Վերջինս էլ սկիզբ է տվել սողունների մյուս բոլոր հայտնի և անհետացած կամ ներկայումս գոյատևող խմբերին: Այս դասին պատկանող բոլոր կենդանիները հասուն վիճակում շնչում են միայն թոքերով:
Հետևաբար նրանց մաշկը չոր է, չի մասնակցում շնչառությանը, պատված է եղջերային թեփուկներով կամ վահանիկներով: Եղջերային ծածկույթը կատարում է պաշտպանական գործառույթ և ապահովում ջրի խնայողությունը՝ նման միջատների արտաքին խիտինային ծածկույթին: Սողունների մաշկի թեփուկային ծածկույթը չի աճում, խանգարում է աճին, իսկ սողունները նույնպես կատարում են մաշկափոխանակություն:
Սողունները ևս ունեն եռախորշ սիրտ և արյան շրջանառության երկու շրջան: Սողունների բեղմնավորումը և զարգացումը կապված չէ ջրային միջավայրի հետ:
Սողունների բեղմնավորումը ներքին է:
Սողունները դնում են պաշարային սննդանյութերով հարուստ, խիտ թաղանթով պատված, խոշոր ձվեր: Զարգացումն ուղղակի է, առանց կերպարանափոխության:
Ուշադրություն
Սաղմնային հատուկ թաղանթների շնորհիվ սաղմը զարգանում է օդային միջավայրում:
Մոտավորապես 180 մլն տարի առաջ երկրագնդի վրա գերիշխում էին սողունների հնագույն տարատեսակները՝ դինոզավրերը: Նրանց ներկայացուցիչները գրավել էին բոլոր կենսամիջավայրերը՝ ջրային, ցամաքային, օդացամաքային:
Ներկայումս սողունները ապրում են հիմնականում տաք ու չոր կլիմա ունեցող երկրներում, քանի որ նույնպես սառնարյուն կենդանիներ են: Այժմ հարմարված են ցամաքային, կիսաջրային և ծովային կենսամիջավայրերում:
Ողնաշարավորների ենթատիպում սողունները բազմաքանակներից չեն, սակայն ունեն միջավայրային հարմարման բազմազանություն: Այժմ հայտնի է մոտ 7,5 հազար տեսակ:
Սողունների մեջ տարբերում ենք` կրիաներ, կոկորդիլոսներ, օձեր, մողեսներ, անհետացած դինոզավրեր:
Միջավայրի պայմաններին հարմարումը հանգեցրել է նրան, որ սողունները ձեռք են բերել տարածության մեջ տեղաշարժվելու տարատեսակ ձևեր և հարմարանքներ: Դրանք իրենց հերթին փոփոխել են սողունների ինչպես վերջույթների կառուցվածքը, այնպես էլ երբեմն մարմինն ամբողջապես: Այսպես.
- Գեկկոնները, որոնք շարժվում են հարթ մակերեսներով, մատների եզրերին ունեն թմբիկաձև ծծիչներ, որոնցով կպչում են պատին:
- Քամելեոնները, որոնք ծառաբնակ են, ունեն ճյուղերից բռնվելու աքցանանման մատներ և պոչի օգնությամբ կարող են կախվել ճյուղերից:
- Թռչող վիշապիկը, որը բնակվում է Մալայան արշիպելագում, մարմնի կողքերին ունի մաշկի լայն ծալք, որի շնորհիվ ծառից ծառ թռչելիս սավառնում է օդում:
- Կրիաները մատների արանքում ունեն լողաթաղանթներ:
- Օձերը բացարձակապես զրկված են վերջույթներից և ունեն որդանման, սողացող մարմին:
Սողունների աչքերն ունեն կոպեր, որոնք ցամաքային միջավայրում խոնավեցնում և պաշտպանում են աչքը: Օձերի և որոշ մողեսների կոպերը միաձուլվել են և դարձել թափանցիկ:
Սողուններին ևս բնորոշ է հովանավորող և նախազգուշացնող գունավորումը:
Առաջինով նրանք ձուլվում են միջավայրին և դառնում աննկատ, իսկ երկրորդով՝ զգուշացնում իրենց վտանգավոր լինելու մասին:
Սողունների տարբեր ներկայացուցիչների մոտ մարմինը ունի խիստ տարբեր կառուցվածքային դրսևորում: Այդ բազմազանությունը պայմանավորված է կմախքի առանձնահատկություններով՝ որպես հարմարման արդյունք:
Այնուհանդերձ սողունների մարմնի ընդհանուր կառուցվածքը դիտարկենք ճարպիկ մողեսի օրինակով:
Մողեսի մարմինը կազմված է միմյանց սահուն հաջորդող գլխից, պարանոցից, իրանից և պոչից:
1. Գլուխ. սահմանազատվում է պարանոցից թմբկաթաղանթներով՝ կրում է տեսողական և լսողական զգայարանները, քթանցքերը, բերանը, գանգատուփում գտնվում է գլխուղեղը:
2. Պարանոց. ապահովում է գլխի շարժուն միացումը իրանին և լավ արտահայտված է:
3. Իրան. սահմանազատվում է պոչից հետանցքով՝ կրում է ուսագոտին և կոնքագոտին, կրծքավանդակը և հիմնական ներքին օրգանները:
4. Պոչ. բնորոշ է գրեթե բոլոր սողուններին, տարբեր տեսակների մոտ ունի տարբեր նշանակություն:
5. Վերջույթներ. բոլոր սողունները, բացառությամբ օձերի, տեղաշարժվում են առջևի և ետևի վերջույթներով:
Ցամաքային կենսակերպով պայմանավորված՝ սողունների կմախքը բավականին նման է երկկենցաղների կմախքին:
Սողունների կմախքը ունի հետևյալ հիմնական բաժինները` I. գանգ, II. ողնաշար, III. գոտիներ, IV. վերջույթներ:
I. Գանգ: Կազմված է գանգատուփից, որը պաշտպանում է գլխուղեղը և ծնոտները: Օձերի ծնոտները կարող են միմյանցից հեռանալ՝ ամբողջական սնունդ կուլ տալու հետևանքով:
II. Ողնաշար: Ունի 5 բաժին՝ պարանոցային, կրծքային, գոտկային, սրբանային, պոչային:
Պարանոցային ողերը մեկից ավել են և միմյանց հետ շարժուն հոդավորվելով՝ թույլ են տալիս գլուխը ազատ պտտել: Կրծքային և գոտկային ողերը միասին 22-ն են և իրենց վրա կրում են գոտիները: Կրծքային և գոտկային ողերին կիսաշարժուն կերպով միացած են կողերը:
Առաջին 5 զույգ կողերը կրծքային հատվածում միանում են կրծոսկրին և ձևավորում կրծքավանդակ:
III. Գոտիներ
Առջևի գոտի՝ ուսագոտի – կազմված է կենտ կրծոսկրից, զույգ անրակից, զույգ թիակից:
Հենարան է հանդիսանում առջևի վերջույթների համար:
Ետևի գոտի՝ կոնքագոտի – կազմված է միմյանց միացած երեք զույգ մասերից:
Հենարան է հանդիսանում հետևի վերջույթների համար:
Բոլոր ողնաշարավորների նման սողուններն ունեն զույգ վերջույթներ՝
- Առջևի վերջույթներ– կենտ բազուկոսկր, զույգ նախաբազկի ոսկրեր, դաստակ, 5 մատներ:
- Ետևի վերջույթներ– կենտ ազդոսկր, զույգ սրունքի ոսկրեր, թաթ, 5 մատներ:
Սողունների բազմացումը և զարգացումը
Սողունների սեռական օրգանները և դիմորֆիզմը
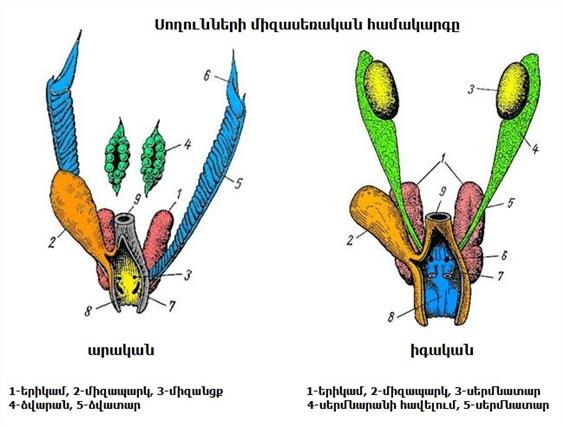
Բոլոր սողունները բաժանասեռ կենդանիներ են և բազմանում են ներքին բեղմնավորմամբ: Սողունների բազմացման օրգանները կառուցվածքով շատ նման են երկկենցաղների բազմացման օրգաններին:
Արուն ունի երկար զույգ սերմնարաններ, որոնք սերմնածորաններով բացվում են կոյանոցի մեջ:
Էգը ունի զույգ ձվարաններ, որոնք ձվատարներով բացվում են կոյանոցի մեջ:
Բազմացման շրջանում զարգացած ձվաբջիջը բեղմնավորվում է սպերմատոզոիդի հետ հենց էգի օրգանիզմում:
Սողունների մոտ լավ արտահայտված է սեռական դիմորֆիզմը: Արուները ունեն վառ գունավորում, ավելի խոշոր են և գրավում են էգերին: Արուներին բնորոշ է նաև մեկ այլ առանձնահատկություն. նրանք բազմացման ընթացքում, օրինակ՝ որոշ մողեսներ, մաշկի վրա, մեջքի երկարությամբ կարող են ձեռք բերել լրացուցիչ կատարներ, թմբուկներ, հավելյալ երանգներ: Այդ ամենը բարձրացնում է արուի գրավչությունը էգի մոտ:
Տարբերում ենք սողունների բազմացման և զարգացման 5 հիմնական փուլ.
- ձվազատում
- բեղմնավորում
- ձվի զարգացում
- ձվադրում
- ուղղակի զարգացում
Ձվազատում
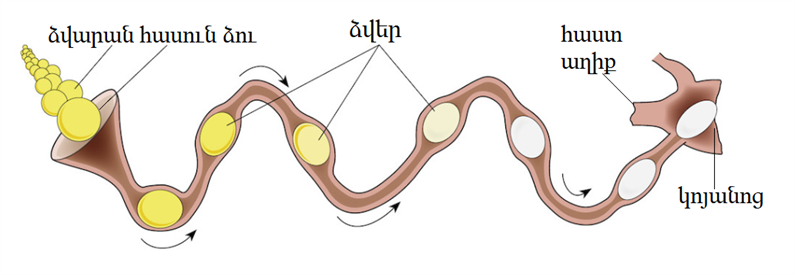
Էգի սեռական օրգաններում՝ ձվարաններում, զարգանում են իգական սեռական բջիջները՝ ձվաբջիջները: Ձվարանից դուրս գալուց հետո ձվաբջիջը ընկնում է ձվատարի վերին, ձագարաձև լայնացած մասը: Ձվատարը ձգվում է մինչև կոյանոց և բացվում դրա մեջ: Կատարվում է հասունացած ձվաբջջի ձվազատում, որը արդյունքում մնում է էգի օրգանիզմում:
Բեղմնավորում
Գարնանը, երբ եղանակը տաքանում է, սկսվում է սողունների բազմացման շրջանը: Զուգավորման ժամանակ արուն սերմնաբջիջները լցնում է էգի կոյանոցը: Կոյանոցից շարժուն սպերմատոզոիդները ձվատարով բարձրանում և թափանցում են ձվաբջիջների մեջ: Ձվատարներում կատարվում է բեղմնավորում: Բեղմնավորումից ձևավորվում է զիգոտ: Զիգոտից սկիզբ է առնում սաղմնավորումը:
Ձվի զարգացում
Բեղմնավորված ձվաբջիջը ձվատարով անցնելու ընթացքում պատվում է մագաղաթանման, ճկուն թաղանթով, օրինակ՝ օձերի և մողեսների մոտ: Կոկորդիլոսների և կրիաների բեղմնավորված ձվաբջիջները պատվում են կրային կճեպով: Ձվատարով շարժվելու ընթացքում կատարվում է բեղմնավորված ձվաբջջից ձվի զարգացման գործընթացը, որը ավարտին է հասնում կոյանոցում:
Սողունների ձուն հարուստ է դեղնուցով և ունի ցամաքի վրա սաղմի զարգացումն ապահովող հարմարանքներ:
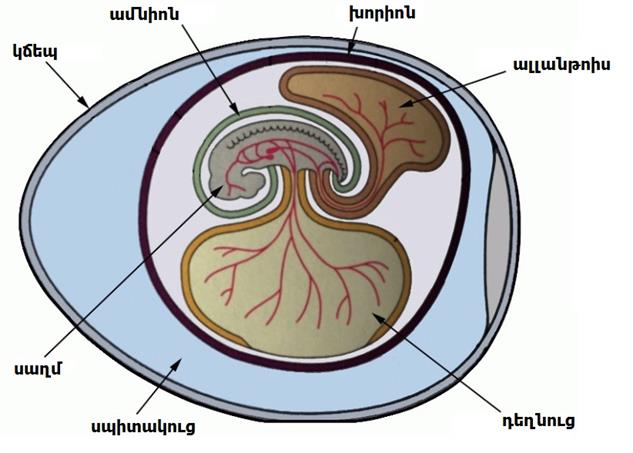
Ձվի կառուցվածքային մասերն են.
- արտաքին ամուր թաղանթ
- սաղմնային թերթիկներ
- դեղնուցապարկ
- սաղմ
Դեղնուցի բաղադրության մեջ կան սաղմի աճման համար անհրաժեշտ բոլոր սննդարար նյութերը: Ձվի թաղանթները պաշտպանում են սաղմը արտաքին ազդեցությունից: Կճեպը ծակոտկեն է, որի շնորհիվ ձուն կատարում է նյութափոխանակություն: Ձվի մեջ՝ սաղմի շուրջ, զարգանում են սաղմնային թաղանթներ. դրանցից մեկը՝ ամնիոնը լցված է հեղուկով և ստեղծում է սաղմի զարգացման համար անհրաժեշտ ջրային միջավայր: Երկրորդ թաղանթը՝ ալլանթոիսը, հարուստ է արյունատար անոթներով և ապահովում է սաղմի շնչառությունն ու արտաթորությունը: Երրորդ թաղանթը՝ խորիոնը, սահմանազատում է սաղմնային մարմինը սպիտակուցային մարմնից և ապահովում դրանց միջև նյութափոխանակությունը: Սպիտակուցը հիմնական կիրառելի սննդային միջավայրն է, որից սաղմը ի վիճակի է կլանել պիտանի նյութեր և արտազատել արգասիքներ:
Ձվադրում
Սողունները ձվերը դնում են ավազի, հողի մեջ, քարերի արանքում, տերևների տակ: Որոշ տեսակների ձվերը մնում են ձվատարում մինչև զարգացման ավարտը: Այդ դեպքում ձագերը դուրս են գալիս ձվերից անմիջապես ձվադրման պահին: Բազմացման այս ձևը կոչվում է ձվակենդանածնություն: Որոշ տեսակների սաղմը զարգանում է մոր ձվատարին ամրացած և պատված չէ ձվային թաղանթներով: Բազմացման այս ձևը կոչվում է կենդանածնություն: Որոշ սողունների արուներն ընդհանրապես չեն հանդիպում, և էգերը բազմանում են առանց բեղմնավորման՝ կուսածնությամբ:
Ուղղակի զարգացում
Լրիվ ձևավորված սաղմը, որը ամբողջական ձևավորված օրգանիզմ է, իր դնչի վրա գտնվող ատամիկով պատռում է ձվի թաղանթը և դուրս գալիս արտաքին միջավայր: Սողունների զարգացումը ուղղակի է՝ առանց կերպարանափոխության: Ձագերը ծնողների խնամքի կարիքը չեն զգում: